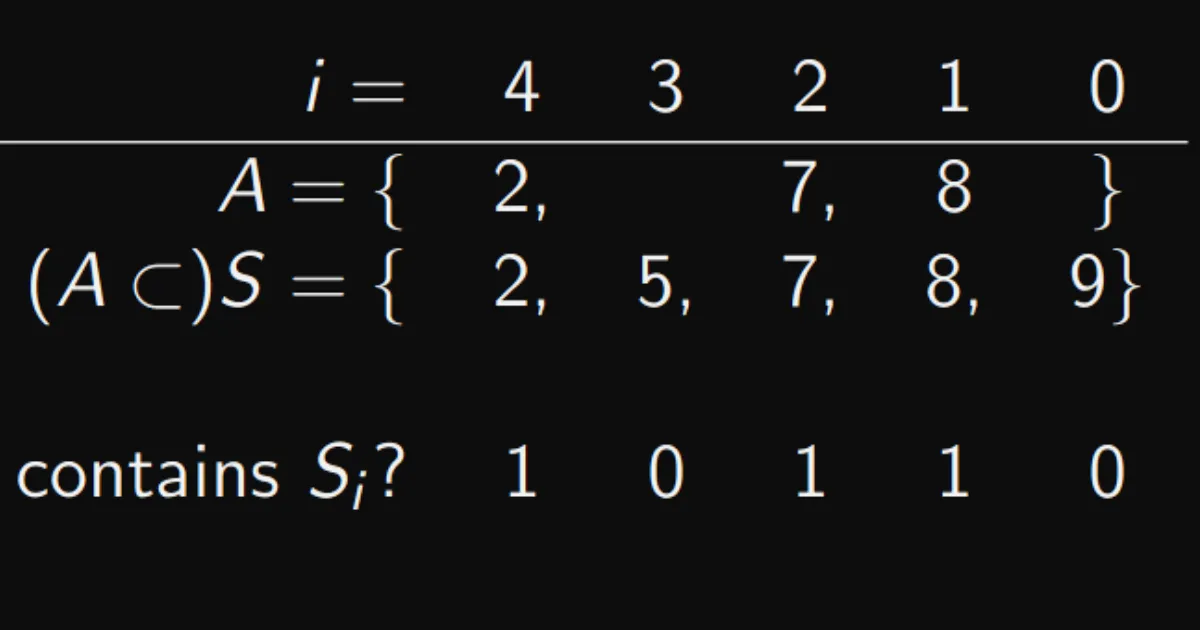Foundations of Algorithms | Manvith Reddy Dayam

Correspondence between Sets and Boolean operators

There exists a correspondence between n-bit numbers and subsets of n element sets.

Function fS , which for a set S containing n elements
• Outputs a unique n-bit number for each subset of S
• Has the property that every n-bit number will correspond to some subset of S
• i.e. fS is a bijection

This will immediately prove that |P(S)| = 2^n , i.e. the power set of any n-element set contains 2n elements

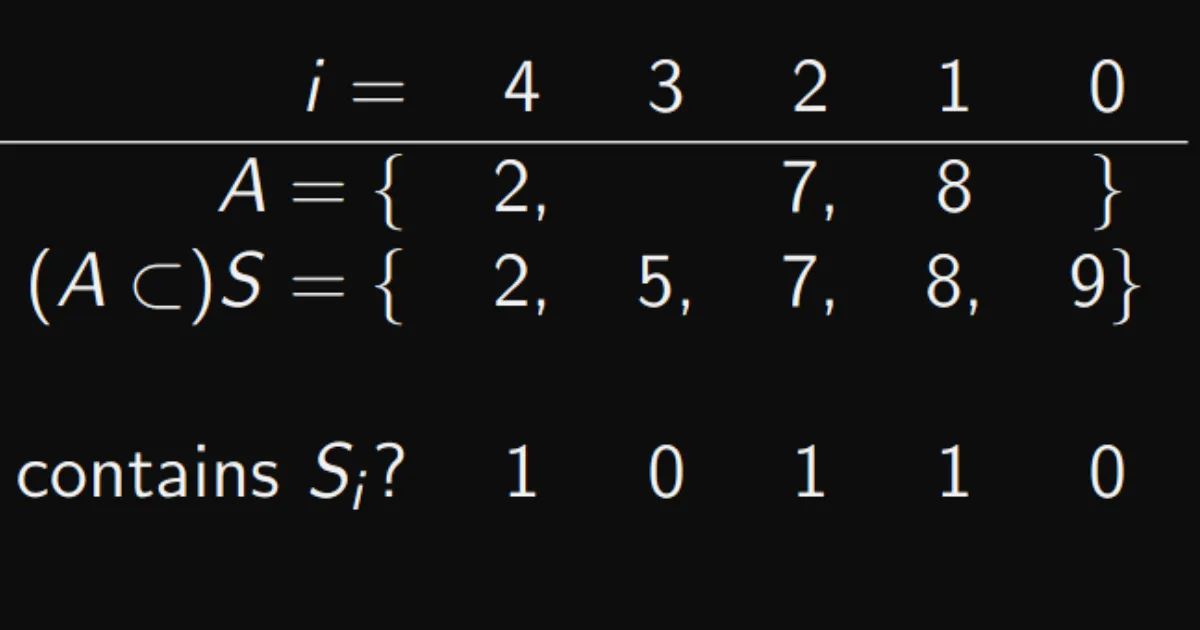
Alt text for the image

Characteristic function of set A, denoted by χA(a) returns 1 if a ∈ A and 0 if a ̸∈ A

A, B \subseteq S \quad (\text{i.e. } A, B \in \mathcal{P}(S))

S = \{ s_i \mid 0 \leq i \leq n - 1 \}

f_S(A) = \sum_{i=0}^{n-1} 2^i \chi_A(s_i)

Importantly, this encoding is unique for each subset A of S, and must be in the range

0 \leq f_S(A) < 2^n

Uniqueness follows from the element ordering Si and their correspondence with bit i in the output number.

This also proves the important property about the length of a power set.

|\mathcal{P}(S)| = 2^n \quad \text{whenever} \quad |S| = n

Now suppose we encode sets A and B as n-bit numbers, respectively, fS (A) and fS (B)

With the superset S, suppose we encode sets A and B as n-bit numbers, fS (A) and fS (B)

f_S(A \cup B) = f_S(A) \lor f_S(B) \\ f_S(A \cap B) = f_S(A) \land f_S(B) \\ f_S(A \triangle B) = f_S(A) \oplus f_S(B)

How does this increase efficiency of set operations?

Suppose we have three sets A, B and C that are subsets of S and we want to compute:

(A \cup B) \cap C

Using traditional data structures, this might involve multiple passes through the elements to build the union of A and B, and then another pass to intersect with C. If there are many elements in 𝑆 and you need to perform this operation multiple times, the cost becomes significant.

Instead..

f_S((A \cup B) \cap C) = (f_S(A) \lor f_S(B)) \land f_S(C)

This expression involves two simple bitwise operations, each of which is performed in constant time, making it highly efficient regardless of the size of the sets or the number of operations required.