Functional Geometry and the Traite de Lutherie (ACM DL)

TRAITE DE LUTHERIE

In 2006, a French luthier named Franc¸ois Denis published Traite´ de lutherie , a comprehensive and seminal treatise which attempted to lay out the manner in which string instrument outlines were constructed.

Renowned makers include, among others, Andrea Amati—recognized as the father of the violin—and distinguished members of his family, Andrea Guarneri and his family (especially son Giuseppe, and Giuseppe “del Gesu”), Matteo Gofriller, Do- minico Montagnana, and the ubiquitous primus inter pares, Antonio Stradivari.

The designs in the book are realized without graph paper, without Vernier calipers, protractors, or just about anything having to do with measurement.

DESIGN PRINCIPLE OF MUSICAL INSTRUMENTS

It is typical for modern makers to copy and modify these old designs. But where did their designs come from? Surely not from an infinite chain of copyists.

The crude design of string instruments is a fairly inevitable consequence of ergonomics: a resonating box, with rounded corners to avoid bumping and blocking, and a concave middle ’waist’ to allow bow access to the strings. But the further refinement of this basic form came from an interaction both musicians and their performance needs, and with the scientific perspective that was emerging simultaneously

In addition, these string instruments took form during an age of scientific revolution—the era of Copernicus, Kepler, Galileo, Newton—where the experimental mindset, with its associated scientific insights, likely had an impact on instrument designers and makers (Schleske 2004).

FUNCTIONAL GEOMETRY

In what way can computational thinking be an intellectual organizing principle for understanding and describing the past, and making sense of the kinds of expertise that flourished and came to maturity?

A set of graphics primitives for realizing outlines of string instruments

The goal of this approach is to mimic accurately the accepted historical traditions for this design, while automating and facilitating the design and the construction process.

Virtually everything is done with an (unmarked) ruler, and a compass, save one fixed dimension. That dimension determines, via entirely proportional constructions, all the other ones.

TYPES

types

-- A point is represented as a tuple of two Doubles (x, y).
type Point = (Double, Double)
 
-- A Geometry type to represent different geometric objects.
data Geometry
  = LabeledPoint String Point
  | LineGeometry Line
  | Circle Point Double
  | Segment Point Point
  | Polygon [Point]
  | Arc Point Point Point
  | Curve [Geometry]
  deriving (Show)
 
data Line = Line Point Point deriving (Show)

FUNCTIONAL GEOMETRY BLOCKS

geometry-functions

intersect :: Geometry -> Geometry -> [Point]
 
-- Intersect two lines
intersect (LineGeometry (Line (x1, y1) (x2, y2)))
          (LineGeometry (Line (x3, y3) (x4, y4))) =
  lineIntersection (x1, y1) (x2, y2) (x3, y3) (x4, y4)
 
-- Intersect a line and a circle
intersect (LineGeometry (Line p1 p2)) (Circle center radius) =
  lineCircleIntersection p1 p2 center radius
intersect (Circle center radius) (LineGeometry (Line p1 p2)) =
  lineCircleIntersection p1 p2 center radius
 
-- Intersect two circles
intersect (Circle c1 r1) (Circle c2 r2) =
  circleIntersection c1 r1 c2 r2
 
-- Intersect two segments
intersect (Segment p1 p2) (Segment q1 q2) =
  segmentIntersection p1 p2 q1 q2
 
-- Default case: Intersection not defined
intersect _ _ = []
 
-- Similarly we have functions for circle-circle 
-- and segment-segment intersection
-- line to line intersection (determinant method)
lineIntersection :: Point -> Point -> Point -> Point -> [Point]
lineIntersection (x1, y1) (x2, y2) (x3, y3) (x4, y4) =
  let denominator = (x1 - x2) * (y3 - y4) - (y1 - y2) * (x3 - x4) -- Denominator of the intersection formulas.
  in if denominator == 0
       then [] -- Lines are parallel
       -- Calculate the x-coordinate of the intersection point.
       else let px = ((x1 * y2 - y1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * y4 - y3 * x4)) / denominator
                -- Calculate the y-coordinate of the intersection point.
                py = ((x1 * y2 - y1 * x2) * (y3 - y4) - (y1 - y2) * (x3 * y4 - y3 * x4)) / denominator
            in [(px, py)]
 
-- line to circle
-- if tangent intersect1 and 2 will be identical
lineCircleIntersection :: Point -> Point -> Point -> Double -> [Point]
lineCircleIntersection (x1, y1) (x2, y2) (cx, cy) r =
  let dx = x2 - x1  -- Direction vector of the line.
      dy = y2 - y1
      -- Quadratic equation coefficients for solving line-circle intersections.
      a = dx^2 + dy^2
      b = 2 * (dx * (x1 - cx) + dy * (y1 - cy))
      c = (x1 - cx)^2 + (y1 - cy)^2 - r^2
      -- Discriminant of the quadratic equation.
      discriminant = b^2 - 4 * a * c
  in if discriminant < 0
       then [] -- No intersection
       else if discriminant == 0
         then -- Tangent case: one intersection point.
           let t = -b / (2 * a)
               intersect = (x1 + t * dx, y1 + t * dy)
           in [intersect]
         else let t1 = (-b + sqrt discriminant) / (2 * a) -- Calculate the two possible solutions
                  t2 = (-b - sqrt discriminant) / (2 * a)
                  intersect1 = (x1 + t1 * dx, y1 + t1 * dy)
                  intersect2 = (x1 + t2 * dx, y1 + t2 * dy)
              in [intersect1, intersect2]
 
 
label :: String -> Point -> Geometry
label name point = LabeledPoint name point
 
yshift :: Point -> Double -> Point
yshift (x, y) dy = (x, y + dy)
 
xshift :: Point -> Double -> Point
xshift (x, y) s = (x + s, y)
 
circle :: Point -> Double -> Geometry
circle center radius = Circle center radius
 
west :: Geometry -> Point
west (Circle (cx, cy) r) = (cx - r, cy)
west _ = error "west: not a circle"
 
south :: Geometry -> Point
south (Circle (cx, cy) r) = (cx, cy - r)
south _ = error "south: not a circle"
 
distance :: Point -> Point -> Double
distance (x1, y1) (x2, y2) =
  sqrt ((x2 - x1) ^ 2 + (y2 - y1) ^ 2)
 
vertical :: Point -> Line
vertical (x, _) = Line (x, -1e6) (x, 1e6)
 
horizontal :: Point -> Line
horizontal (_, y) = Line (-1e6, y) (1e6, y)
 
verticalGeometry :: Point -> Geometry
verticalGeometry (x, _) = LineGeometry (Line (x, -1e6) (x, 1e6))
 
horizontalGeometry :: Point -> Geometry
horizontalGeometry (_, y) =
  LineGeometry (Line (-1e6, y) (1e6, y))
 
-- The pointfrom function computes a point at a fraction t between two points
pointfrom :: Point -> Point -> Double -> Point
pointfrom (x1, y1) (x2, y2) t =
  (x1 + t * (x2 - x1), y1 + t * (y2 - y1))
 
-- The upperCircle function returns a circle that is:
-- Tangent to the inner circle (centered at centerInner).
-- Tangent to the outer circle at the given targetPoint.
upperCircle :: Geometry -> Double -> Point -> Geometry
upperCircle (Circle centerInner radiusInner) outerRadius targetPoint =
  let tangentRadius = abs (outerRadius - radiusInner)
      possibleCenters =
        intersect
          (Circle targetPoint tangentRadius)
          (Circle centerInner (tangentRadius + radiusInner))
  in case possibleCenters of
       [center] -> Circle center tangentRadius
       _ -> error "Could not compute upper circle"
upperCircle _ _ _ =
  error "upperCircle expects a Circle as the first argument"

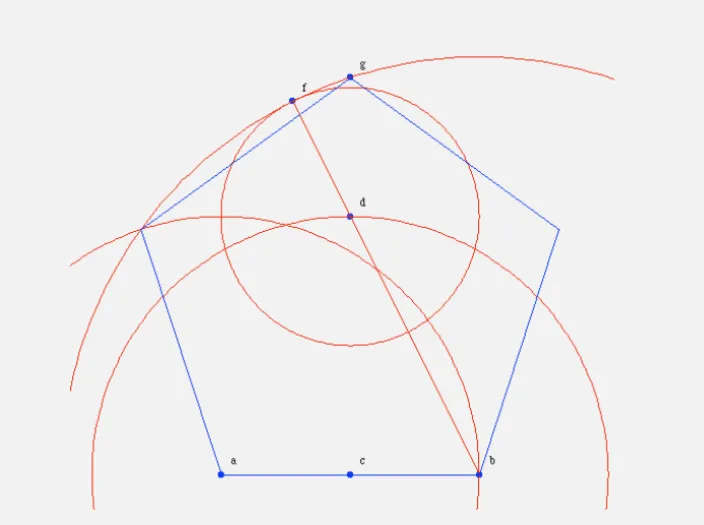
PENTAGON

Pentagon from this primitives.

pentagon

pentagon :: Point -> Double -> [Geometry]
pentagon a s =
  let
    -- Point b: Shift point a by s horizontally
    b = xshift a s
 
    -- Point c: Intersection of circles centered at a and b, and the line a-b
    c = case intersect (circle a s) (circle b s) of
          [p1, p2] -> case intersect (LineGeometry (Line a b)) (LineGeometry (Line p1 p2)) of
                        [p] -> p
                        _   -> error "Failed to compute point c"
          _ -> error "Failed to compute point c"
 
    -- Point d: Topmost point of the intersection of vertical line through c and circle centered at c
    d = case intersect (circle c s) (LineGeometry (vertical c)) of
          []  -> error "Failed to compute point d"
          pts -> top pts
 
    -- Point f: Topmost point of the intersection of line b-d and a circle centered at d
    f = case intersect (circle d (distance a c)) (LineGeometry (Line b d)) of
          []  -> error "Failed to compute point f"
          pts -> top pts
 
    -- Point g: Topmost point of the intersection of vertical line through c and circle b-f
    g = case intersect (circle b (distance b f)) (LineGeometry (vertical c)) of
          []  -> error "Failed to compute point g"
          pts -> top pts
 
    -- Points p and q: Leftmost and rightmost points of intersections of circles centered at g, a, and b
    p = case intersect (circle g s) (circle a s) of
          []  -> error "Failed to compute point p"
          pts -> left pts
 
    q = case intersect (circle g s) (circle b s) of
          []  -> error "Failed to compute point q"
          pts -> right pts
 
  in
    [ label "a" a
    , label "b" b
    , label "c" c
    , label "d" d
    , label "f" f
    , label "g" g
    , label "p" p
    , label "q" q
    , LineGeometry (Line b f)
    , circle a s
    , circle c s
    , circle d (distance d f)
    , circle b (distance b f)
    , Polygon [g, p, a, b, q, g]
    ]

Pentagon

LUTE ZWOLLE

One of the earliest lutes.

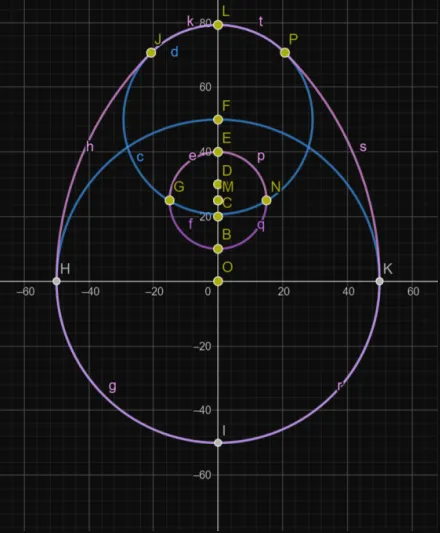
lute-zwolle

luteZwolle :: Double -> [Geometry]
luteZwolle rad =
  let
    -- Base definitions
    origin = (0, 0)
    c = Circle origin rad
    d = 2 * rad
 
    -- Key points on the left-hand side
    p = (-rad, 0)       -- West of the circle
    q = (0, rad)        -- North of the circle
    qprime = (0, -rad)  -- South of the circle
 
    -- Intersect to find r
    r = case intersect (Circle (mirror p) d) (LineGeometry (Line (mirror p) q)) of
          (pt:_) -> pt
          _      -> error "Failed to compute point r"
 
    -- Point s
    s = yshift q (distance q r)
 
    -- Rose circle on the left-hand side
    roseCenter = (0, rad / 2)
    roseRadius = (3 / 10) * rad
    rose = Circle roseCenter roseRadius
 
    -- Left-hand side arcs
    leftArcs =
      [ Arc roseCenter q (west rose)
      , Arc roseCenter (west rose) (south rose)
      , Arc origin p qprime
      , Arc (mirror p) p r
      , Arc q r s
      ]
 
    -- Mirrored right-hand side arcs
    rightArcs = map mirrorArc leftArcs
 
    -- Generate map points for the rose
    mappedPoints =
      concatMap
        (\t ->
           [ LabeledPoint "" (pointfrom origin q t)           -- Left-hand side
           , LabeledPoint "" (mirror (pointfrom origin q t))  -- Mirrored
           ])
        [0, 0.2, 0.4, 0.6, 0.8, 1.0]
 
  in
    mappedPoints ++ [c, Circle q (distance q r)] ++ leftArcs ++ rightArcs

HARMONIC AND SUB-HARMONIC SECTIONS

Harmonic Section

A harmonic section divides a line (s and m) into two parts such that the ratio of the larger segment to the smaller segment is the same as the ratio of the whole line to the larger segment.

Subharmonic Section

A subharmonic section is a related geometric construction used by luthiers to obtain practical, compass-only rational approximations of the ideal harmonic division. Where a harmonic section divides a line into two parts s and m satisfying (larger / smaller) = (whole / larger), the subharmonic construction produces a sequence of simple rational ratios that converge to the same ideal proportion but are easier to produce by hand with a fixed-span compass.

Framework for Lute Geometry

The lengths s and m, derived from the line, are used to construct circles that define the shape and structure of the lute proportions that are rational approximations of the harmonic section.

APPROXIMATE PENTAGON

We use a “rusty compass” that cannot change dimension) as long as we can draw perpendicular lines. Then, common carpenter’s tricks let us code the pentagon with rational, Pythagorean approximants. We use 14/9, 3/10, 20/21

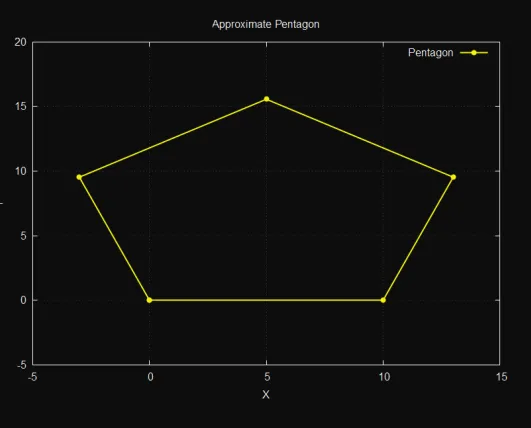
approx-pentagon

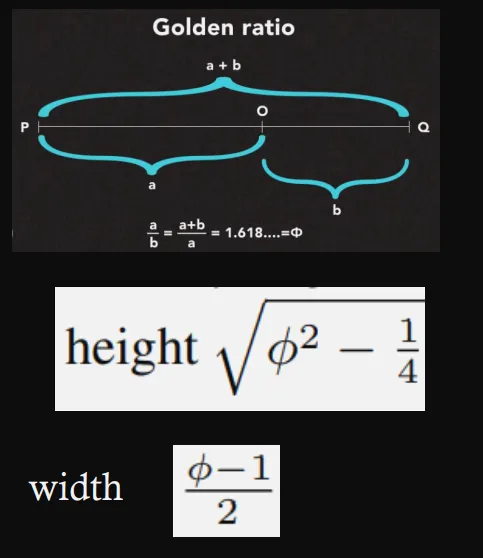
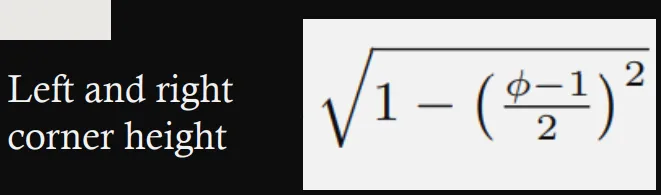
approx-pentagon-info approx-pentagon-info2

approx-pentagon

-- a - starting vertex s - side
approximatePentagon :: Point -> Double -> [Geometry]
approximatePentagon a s =
  let
    -- Compute key points
    b = xshift a s
    t = yshift (midpoint a b) (s * (14 / 9))
    d = yshift (xshift b (s * (3 / 10))) (s * (20 / 21))
    c = yshift (xshift a (-s * (3 / 10))) (s * (20 / 21))
  in
    -- Connect the points to form the pentagon
    [ Segment a b
    , Segment b d
    , Segment d t
    , Segment t c
    , Segment c a
    ]

APPROXIMATE LUTE

The length of the lute is 3m+ 2s, where m and s are the radii of circles derived from carefully constructed geometric sections.

The highlighted box to the left of the vertical axis of the lute contains a harmonic section, and that to the right, a subharmonic section.

Let s+m = 1 : then a better approximation is s0 = m and m0 = s + 2m. Solving s/ m = s 0 /m0 gives s = 1− √1 /2 , the smaller part of the section. Beginning with s = m = 1, we get the series of approximants 1/3 , 3/7 , 7/17 ; luthiers would use initial terms from this series (and those like it) as approximations of its limit. Such constants are mentioned in Arnault’s manuscript

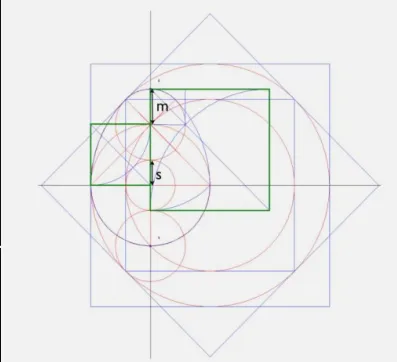
approximate-lute

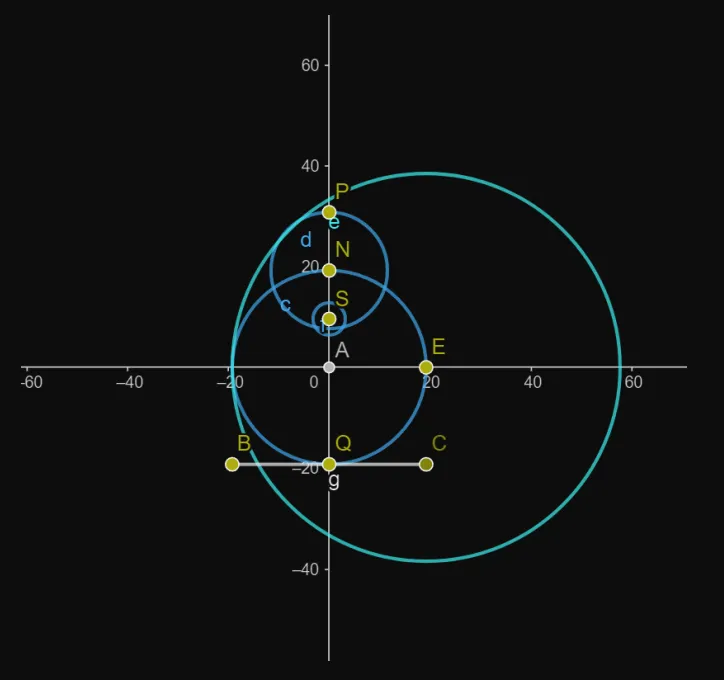
approx-lute

-- Approximate Lute Function
approximateLute :: Double -> Double -> Double -> [Geometry]
approximateLute s m l =
  let
    -- Total length of the lute
    n = 2 * s + 3 * m
 
    -- r: scaling factor
    r = l * ((m + s) / n)
 
    -- Key points
    origin = (0, 0)
    q = yshift origin (-r)
    p = yshift q l
 
    -- Main circle
    cmain = Circle (yshift q r) r
 
    -- Top circle
    northCmain = yshift (yshift q r) r
    ctop = Circle northCmain (distance northCmain p)
 
    -- Right circle
    eastCmain = xshift (yshift q r) r
    cright = Circle eastCmain (2 * r)
 
    -- Bridge segment
    bridgeY = l * (s / n)
    bridge = Segment (xshift q (-r)) (xshift q r)
 
    -- Sound hole
    sPoint = yshift p ( - (l * ((s + 3 * m) / (2 * n))) )
    rs = distance sPoint (xshift eastCmain (-r)) / 3
    sh = Circle sPoint rs
 
    -- Curve connecting components
    curve = Curve [cmain, cright, ctop]
  in
    [ -- Points
      LabeledPoint "Origin" origin
    , LabeledPoint "Q" q
    , LabeledPoint "P" p
    , LabeledPoint "North of Main Circle" northCmain
    , LabeledPoint "East of Main Circle" eastCmain
    , LabeledPoint "Sound Hole Center" sPoint
 
      -- Circles
    , cmain
    , ctop
    , cright
    , sh
 
      -- Segment
    , bridge
 
      -- Curve
    , curve
    ]

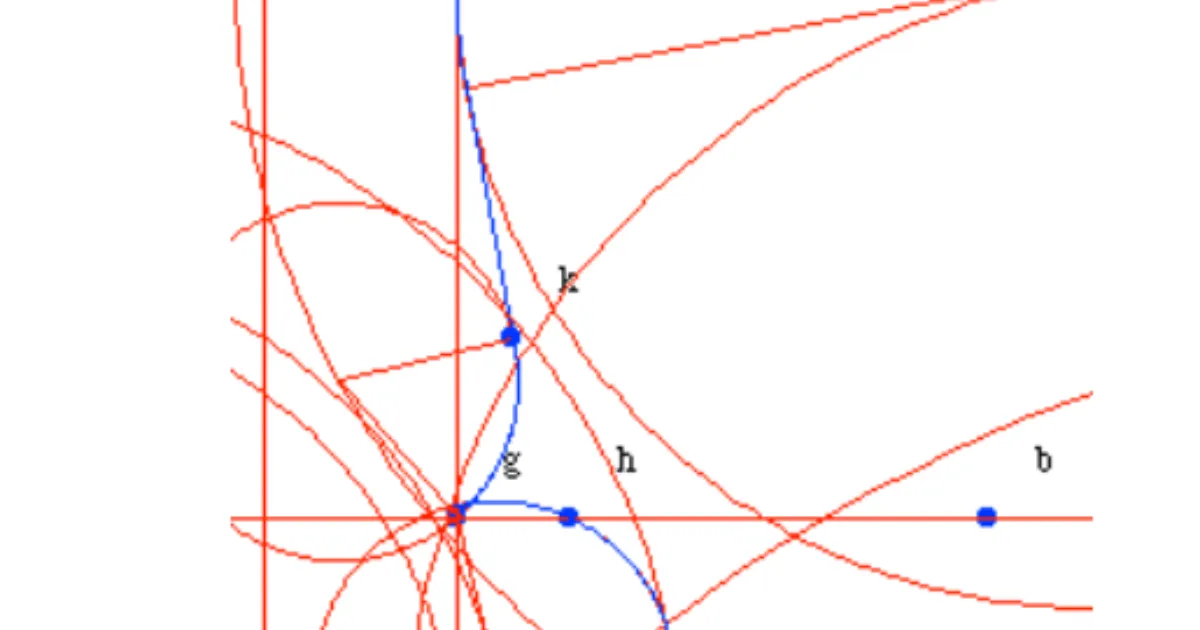
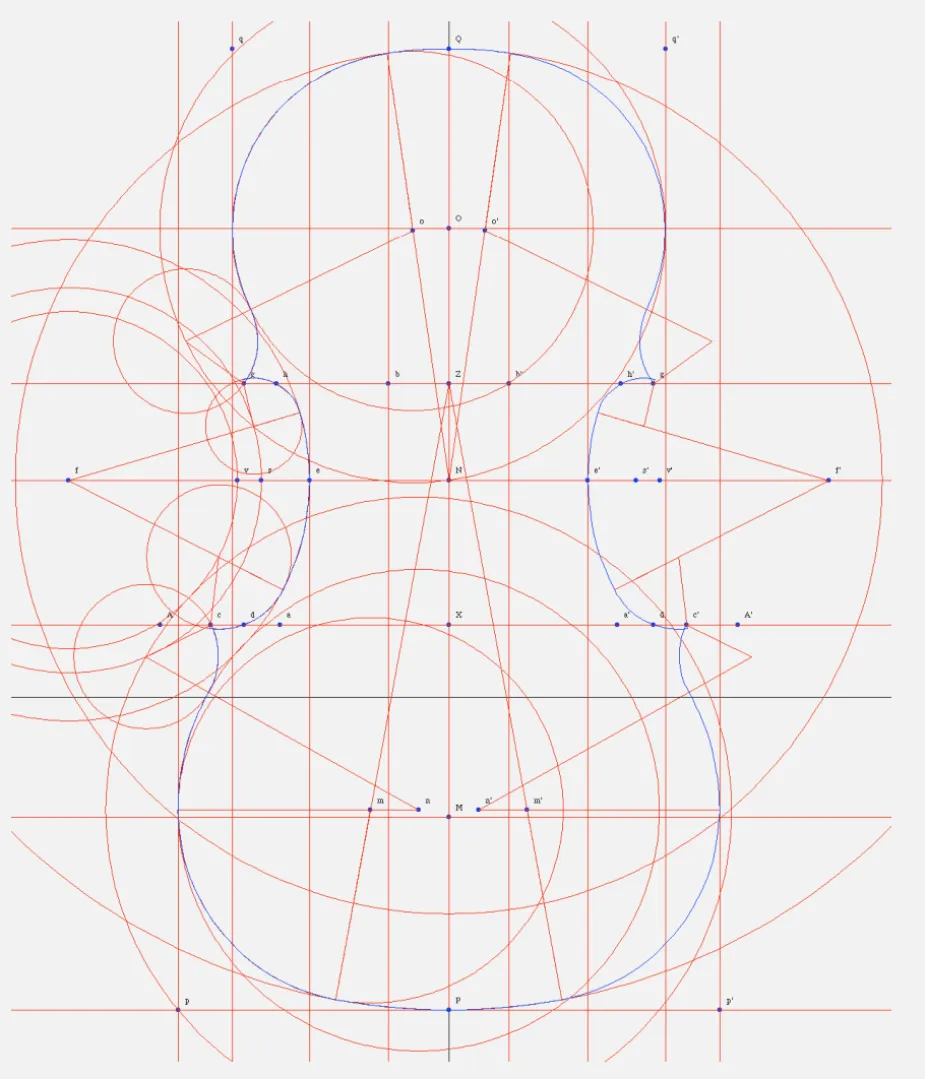
AMATI VIOLIN

• The outline has four essential parts: the framework, which blocks out the regions, and the upper, lower, and middle bouts.

• A key feature of the outline is that it is parameterized by only one fixed dimension: the distance XQ from the top of the outline to the top of the lower bout

amati-violin

helper-geometries

-- Function to add a parameter to both coordinates of a point
addToPoint :: Point -> Double -> Point
addToPoint (x, y) param = (x + param, y + param)
 
-- calculate negative slope point
negSlopePoint :: Point -> Point
negSlopePoint (x,y) = (x + 1, y - 1)
 
-- Given a large
-- circle C , a radius r, and a
-- point p, where is the circle of radius r located that is tangent to the
-- outer side of C, and also tangent to p
reverseCurve :: Geometry -> Double -> Point -> [Geometry]
reverseCurve (Circle centerInner radiusInner) outer pt =
  let outerRadius = abs (outer - radiusInner)
      pts = intersect
             (Circle pt outerRadius)
             (Circle centerInner (outerRadius + radiusInner))
  in map (\p -> Circle p outerRadius) pts

amati-violin